To understand the physics relating to supposed greenhouse gas warming you need to understand the Stefan-Boltzmann Law.

The Stefan-Boltzmann Law in physics enables us to determine not only the outward radiative flux from a body at a certain temperature, but also the maximum equilibrium temperature that any given single source of radiation could achieve in a target.  There are online calculators such as here to which you may wish to refer.  If you enter one (1) for both the emissivity and the area, then you can enter either the radiative flux or the temperature, typing an x for the unknown one.  

The flux is proportional to the fourth power of the absolute temperature.  So, the first point we need to consider is due to the fact that the fourth power of the mean of a set of positive numbers is always less than the mean of the fourth power of each of those numbers.  For example, the mean of 3, 4 and 5 is 4 and its fourth power is 256.  But the mean of the fourth powers of each number is over 320.  Hence the temperature achieved by variable flux with a given mean is always colder than the temperature achieved by a uniform flux equal to that mean.  This is the first point overlooked by climatologists when they attempt to quantify surface temperatures.  If the mean solar flux to the Moon is about 340w/m^2 then calculations give us about 278K which is about 5°C but measurements indicate the mean is well below that.  For Earth it would be even colder because the atmosphere absorbs or reflects about half the incident solar radiation.

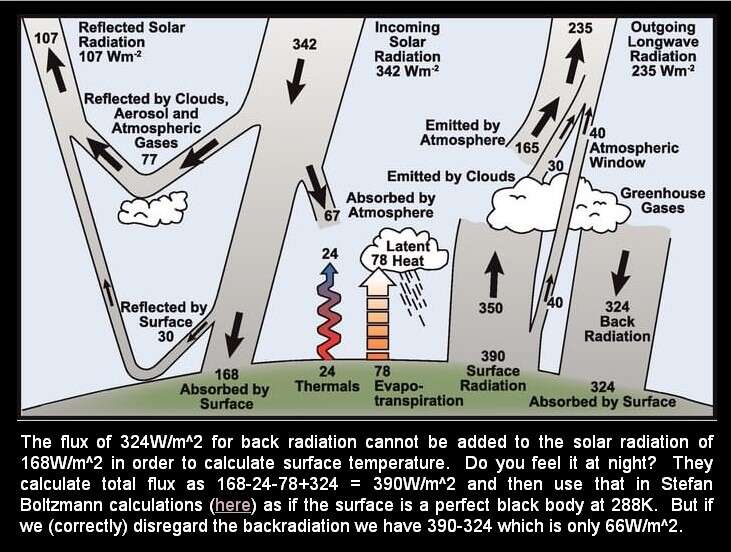
You might think that you can explain a higher temperature using a lower value for emissivity, such as 0.8.  But if that is the case, then 20% of the incident radiation is reflected, so you must reduce that figure accordingly.  So, you will get the same answer.  For example, a polished silver plate may have an emissivity of only 0.2 (meaning it reflects 98%) but it won’t get hotter in the Sun than a black asphalt road. Energy diagrams usually show about 168w/m^2 to 170w/m^2 for the solar radiation entering the Earth’s surface after some reflection by the surface.  If you use the online Stefan-Boltzmann Law calculator that gives about 233K (-40°C) or 234K.  But, because it is variable flux, the maximum global mean surface temperature that the solar radiation could achieve is probably even colder than -50°C.  Climatologists don’t seem to know this.

But there is yet another very important point to make:  the Stefan-Boltzmann Law only ever gives the correct temperature for a single source of radiation.  No published experiment anywhere in world literature confirms that it gives correct results for two or more radiative fluxes from different sources that are just added arithmetically.  The law is derived for a single source only.  It would be very easy to design a simple experiment that would support the contention by climatologists that the law can be used for multiple sources.  But can anyone here find such an experiment?  In fact, the assumption can be proved wrong in your backyard on a calm night with a thermometer, some electric-bar radiators and a few extension cords.

How do we know climatologists do this?  One only has to look at their energy diagrams.  In these diagrams is a grossly overstated figure for back radiation which has clearly just been a calculated value (not measured) so as to, they think, give the right answer.  They add to solar radiation of about 168 to 170w/^2 about 340w/m^2 of back radiation. They then deduct just over 100w/m^2 of non-radiative cooling and then they use the net figure of just over 390w/m^2 to get about 288K (15°C) as the global mean surface temperature.  Not only is it completely wrong to use the net flux, but they also overlooked the fact that it is variable so the mean would be more like 0°C.  See http://climate-change-theory.com for the detailed calculations.

What really causes the surface to be far warmer than that which direct solar radiation could achieve is the input of thermal energy via the “heat creep” process which has nothing to do with radiation or any greenhouse gases.  It is actually these gases that cool all the other molecules that comprise about 99% of the troposphere.  These molecules collide with water vapor, carbon dioxide, methane and similar molecules that are the only ones able to radiate the energy acquired from all the nitrogen, oxygen, argon and other non-radiating molecules, thus acting like holes in a blanket.  None of the energy in the downward radiation gets converted to thermal energy in warmer regions of the surface.

For more on this read my peer-reviewed paper “Radiated Energy and the Second Law of Thermodynamics” and then, to learn what actually happens, read “Planetary Core and Surface Temperatures.” Over 20,000 have read my papers without anyone publishing a valid refutation to my knowledge: correct me if I’m wrong.  The papers are on Researchgate and elsewhere, with the main six able to be downloaded free at https://ssrn.com/author=2627605 all of which I recommend reading.  By all means, discuss the content here.